Estimation of a flexible demand model
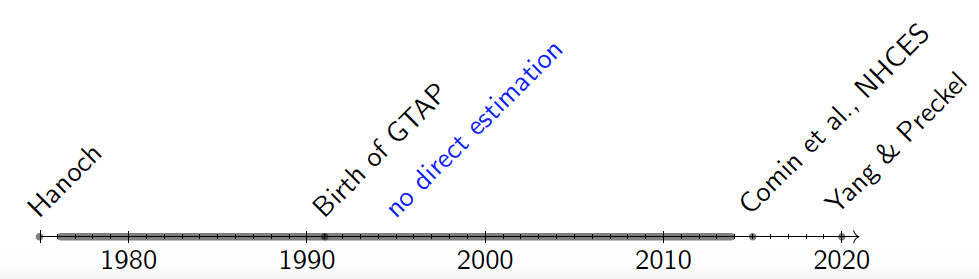
In 1975, Giora Hanoch published a seminal paper in Econometrica which introduced a relatively flexible demand system called the constant difference of elasticities (CDE). The model is a generalization of the CES. It is non-homothetic, has non-constant elasticities, globally well-behaved, and separates substitution effects from income effects. These features, particularly the global regularity, attracts economists who use computable general equilibrium (CGE) models. In the past, the CDE demand model has more or less influenced the research outcomes of at least 30,000 researchers worldwide who use CGE models to analyze global policy issues using the GTAP database and parameter files, and many more who use other CGE models, such as EPPA, MIT JPGC, Envisage and MANAGE.
However, the direct estimation of the CDE has proven to be difficult due to complexities of the model. Unlike other scientists where essential dataset can be observed exogenously, economists often confront data obstacles when it comes to utilities, which thwart identification using reduce-form approaches. For this reason, the CDE as demand model has never been directly solved in the past 45 years. Among these years, Comin et al. (2015) structurally estimate a model that is implicitly direct which is close to a CDE but still lacks several critical features as in the CDE.
Since Anton Yang started his Ph.D. studies at Purdue, he has quickly become interested in theoretical demand models and their applications in structural economic and geography models using computational methods. Partially funded by the Center for Global Trade Analysis (GTAP), Anton began his journey of theoretical and empirical research on the CDE at the GTAP Center, where he also has worked with his co-chairs Dr. Thomas Hertel and Dr. Russell Hillberry, as well as Dr. van der Mensbrugghe on a few related subjects, and learned different types of knowledge that helped him “assemble the gears” later on. From 2019 to 2020, Anton conducted a two-year independent study of computational methods for optimization and advanced mathematical programming supervised by Dr. Paul Preckel. Throughout the time, they focused together on using optimization methods to identify unique solutions of economic models, and seek to apply the numerical methodology to tackle the CDE problem.
In June, 2020, they found solutions to the parameters of the CDE for the first time, and presented virtually in their organized session at the Annual Conference on Global Economic Analysis. In this work, they provide a direct estimation approach to estimate an implicit additive demand model - an empirical demand puzzle. They show that there are minor discrepancies in the demand theory that relates to parameter boundaries in Hanoch (1975). Meanwhile, they prove that the stated global regularity conditions in the theoretical demand model can be slightly relaxed, and that the relaxed parametric conditions facilitate estimation. They also introduce a normalization scheme that is beneficial for the scaling of the parameter values and which appears to have little impact on the economic performance of the estimated system. Furthermore, they design a new optimization strategy to assess the robustness of parameter estimates by developing a systematic procedure to determine the latitude for changing parameters.
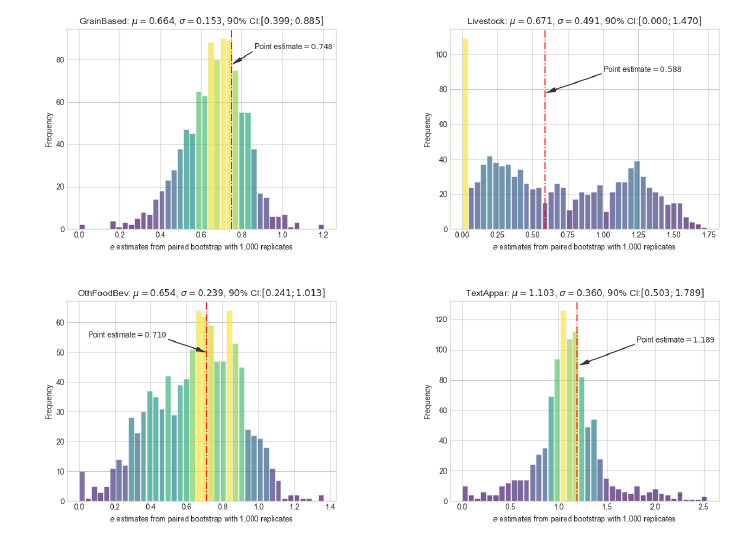
After examined parameter estimates from paired bootstrap with 1,000 replicates, they discussed these results together with Purdue econometrician Dr. Michael Delgado, and concluded that some of the bootstrapped distributions appeared to be more uniform than normal. By law of large numbers, they would expect the distributions to be normal, since the estimator is asymptotically normal. This led them to look for possible multicollinearity issues in the structural problem, while thinking more carefully along the lines of possible suffering from a small-sample bias.
For these reasons, Anton initiated and drafted a research proposal to the World Bank, with other Principal Investigators Dr. Thomas Hertel, Dr. van der Mensbrugghe and Dr. Preckel, and requested World Bank's confidential disaggregated data and metadata for both the 2011 and 2017 rounds of the International Comparison Program (ICP). The World Bank approved the proposal in December, 2020 and sent the unpublished data to the team. These unpublished data are the key for two reasons - one empirical and one computational. From a strictly empirical point of view, they seek to incorporate the most accurate estimates of international cross-section variation in consumer prices in the CDE estimation. From a computational point of view, they seek to obtain a feasible mathematical/numerical solution to the relatively flexible demand model. The set of unpublished disaggregated data allows to check the detailed data matrices for the eigensystems to ensure the estimated standard errors are estimated consistently and that there are no potential multicollinearity or other numerical problems.
Phase II
Bringing the study to the next phase, the team will now show the users of the CGE community how the estimated CDE parameters might affect policy analysis and projection via the applications. There are two types of applications, which includes a 10 to 15 years’ income projection and a trade frictions scenario. The projection scenario employs an updated Shared Socioeconomic Pathways (SSPs) database with global GDP and population forecast. The trade frictions scenario is based on the tariff. The first one involves a forward-looking projection of the global economy, which will exercise the income elasticities of demand - which evolve with per capita income under the CDE demand model. The second one will exercise the price elasticities of demand , which also vary as a function of expenditure shares using the CDE.
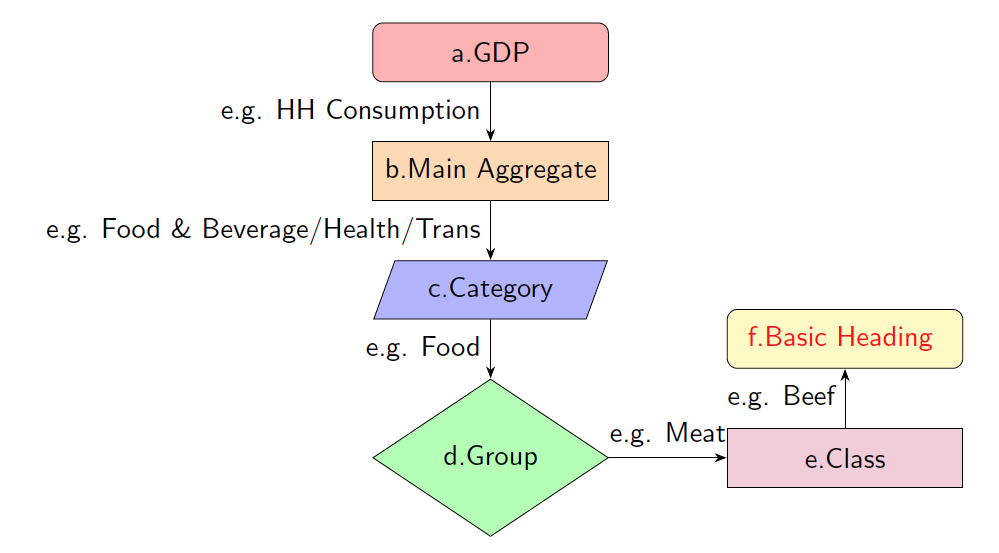
The immediate use of the confidential ICP data will be for the explanatory unit-cost variables in the CDE model. The econometric exercise will then exploit the ICP-based cross-commodity price variations (using the classification of Basic Heading) along with national and regional income differences. The demand theory suggests that any implicitly additive models are generally more appropriate for commodities defined broadly at aggregate levels. This is because that there is always a proportional relationship between goods k's substitution characteristics and the Allen-Uzawa partial elasticities of substitution between goods k and m. For this reason, the team uses the detailed ICP information to construct matrices of price variations across 10 commodities at an aggregate level that is similar to what has been categorized in Reimer and Hertel (2004). At the end, We expect the detailed ICP data to help us produce consistent estimates, as well as measures of robustness, again, via bootstrapping.
We expect our research findings to be one of the major contributions that improve contemporary CGE analysis. The application of the estimated CDE parameters for the first time in the GTAP Model will likely affect the simulation results produced by the world’s many major think-tanks and institutions who conduct quantitative analysis of international economic policy issues and answer important questions to policymakers.
Potential future directions
In the future, we will be seeking opportunities to collaborate with Professor Will Masters at Tufts University on his efforts to create a new “food price data hub” within the World Bank data group, for computing price levels for each of the GTAP agricultural and food sectors. We also hope to pursue potential nutritionally-relevant research jointly with Professor Masters’ group at Tufts University. Another effort to make is to improve ICP's expenditure weights (within Groups) to calculate PPPs and infer quantities from the value flows.
Finally, our computational methods can be applied outside the demand system studies, and are not limited in trade, economic geography, or industrial organization. These identification techniques would be well-suited in agricultural and resource economics, as well as in other economics, science and interdisciplinary disciplines, where numerical methodologies and mathematical optimizations are useful to identify unique solutions of scientific models that are used in understanding deep analytical frameworks.