Graph Neural Network in Space: A New Gravity Explanation of Continuous Trade (with Yang Yu)
The structural gravity models of trade integrate the like of Newton’s Law of universal gravitation with different economic motivations of general equilibrium models. The key advantage of these workhorse models of international trade is that they can relatively consistently fit the data on bilateral trade flows, while allowing to succinctly perform counterfactual analysis of applied policy interests. However, the role of neighboring locations of origins and destinations and its effect on bilateral trade flows are not accounted for in traditional gravity models where bilateral geographical barriers increase the size of implied trade costs hence impede trade between the same bilateral trade partners. This paper introduces graph neural network (GNN) into gravity model of trade and uses recent deep learning techniques to provide an alternative explanation of gravitational patterns of international trade flows in a geospatial framework. Unlike traditional machine learning algorithms including neural networks which typically apply to data that lie in Euclidean spaces, GNN operates on interpretable graph domain, thereby making good use of unique non-Euclidean data structure. These spatial characteristics reveal sequentially the hidden factor between country nodes and trade flows from the representation of neighborhood matrices and automatically provide a new rationale for gravity. We study interpretation approaches to interpreting model components after the model is well-learned (i.e., post-hoc interpretability analysis) and focus on the improved gradients with respect to endogenous variables (to obtain the saliency of shocks) in counterfactual analyses of most computable general equilibrium models. We use these interpretation methods to measure the welfare gains of trade.
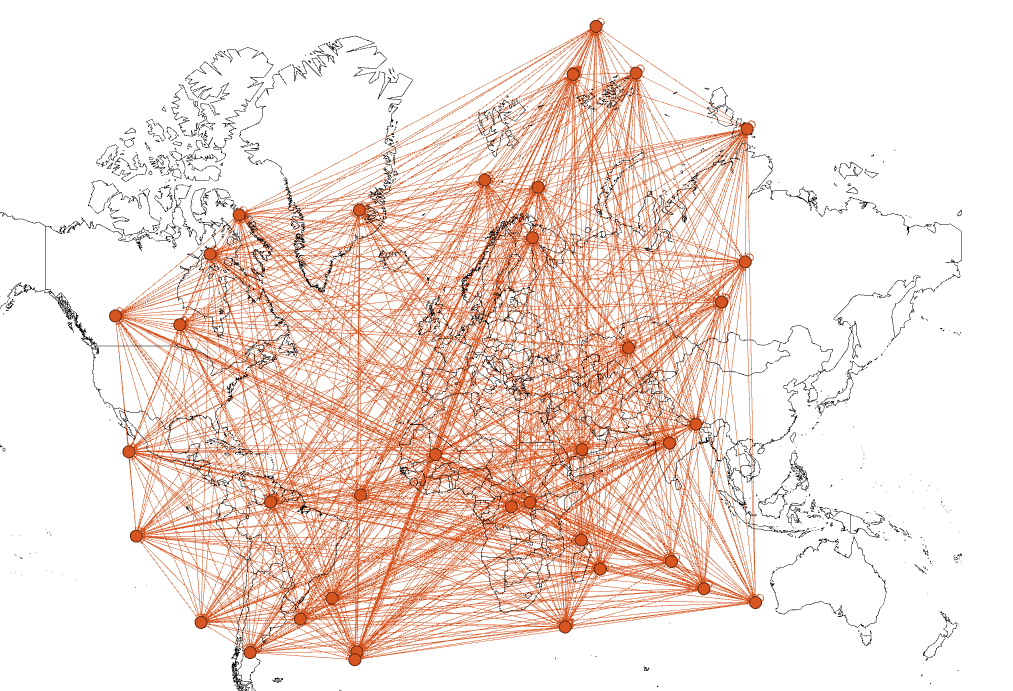
Figure 1. Trade Flows in Space (37 WIOD Countries, 1995).
Wohl and Kennedy (2018) compares the out-of-sample predictions of trade flows using the World Bank and gravity data (i.e., COMTRADE and CEPII) provided by Yotov (2016) and the root mean square error across the gravity models (OLS and PPML estimators) and traditional NN. They find that the NN algorithm outperforms the standard gravity models.
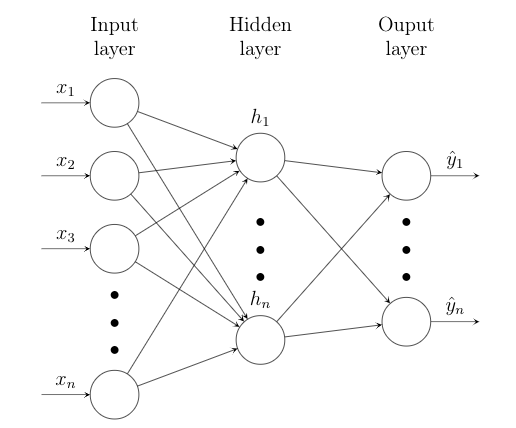
Figure 2. Traditional NN with One Hidden Layer.
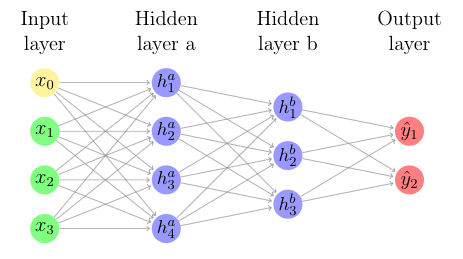
Figure 3. Traditional NN with Two Hidden Layers.
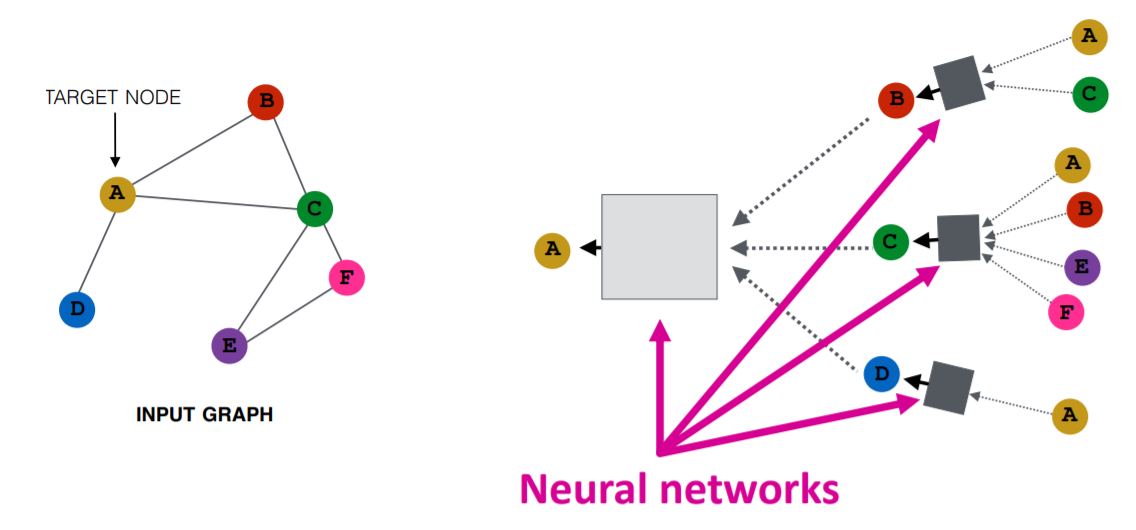
While NNs improve the accuracy of the out-of-sample predictions by allowing high non-linearity of inputs and larger model space, they still operate on Euclidean data and does not consider the effects of neighborhoods of country nodes on trade flows. GNNs, on the other hand, are graph based and reveal the effects of hidden states among countries on bilateral trade. In Figure 4, node A captures information from its neighborhoods (nodes B, C, D) and the neighborhoods of neighborhoods (node B --> nodes A and C, node C --> nodes A, B, E, and F, and node D --> node A, which is itself). The GNN updates the hidden state of A using weighted average of the information of A's neighborhoods.
Figure 4. GNN and Neighborhoods of Node A.
Source: Purvanshi Mehta, Graphs Neural Networks in NLP, Neural Space, 2020.
Table 1. Illustration of a base model.
Table 2. Selected interpretation methods.
We study interpretation approaches to interpreting model components after the model is well-learned. This is also called post-hoc interpretability analysis. The concept of gradients of inputs is similar to counterfactuals in a structural framework of general equilibrium. We say that it is the saliency of shocks and focus on the improved gradients with respect to endogenous variables.
The ad-hoc modeling is to induce economic models into the GNN modeling. We use economics-induced graph neural network as an application to gravity estimation and study the non-Euclidean data-driven size of implied trade costs and welfare gains of trade.
The ad-hoc modeling is to induce economic models into the GNN modeling. We use economics-induced graph neural network as an application to gravity estimation and study the non-Euclidean data-driven size of implied trade costs and welfare gains of trade.